
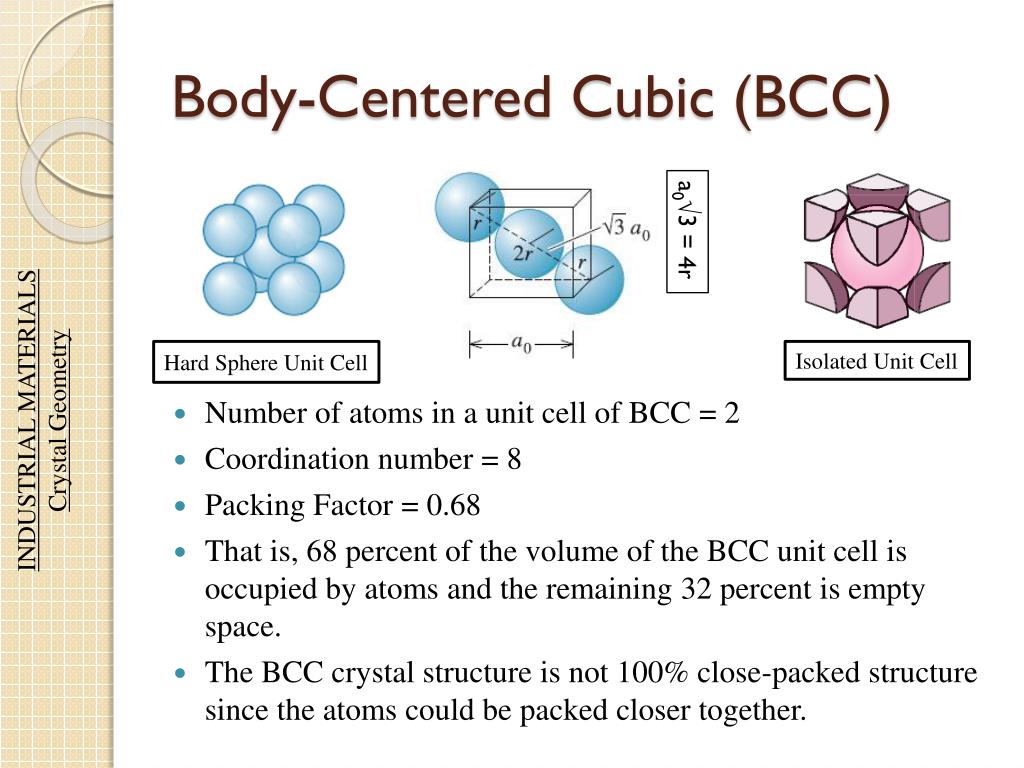
Therefore, we can derive the number of atoms in an FCC lattice through the below derivation: 8 × 1 8 + 6 × 1 2. The difference to the next plane, the A plane, is again √ 6 r2 / 3 in the z-direction and a shift in the x and y to match those x- and y-coordinates of the first A plane. This means that one unit cell contains only 1 2 the volume of an atom. Carl Friedrich Gauss proved that the highest average density – that is, the greatest fraction of space occupied by spheres – that can be achieved by a lattice packing is The volume of each atom is (4R3) and the volume of the unit cell is. In geometry, close-packing of equal spheres is a dense arrangement of congruent spheres in an infinite, regular arrangement (or lattice). The packing factor is the fraction of space occupied by atoms, assuming that atoms are hard spheres Packing factor Examplele 1.3 Calculate the packing factor for the FCC cell There are 4 lattice points per cell and one atom per unit cell giving total 4 atoms per unit cell. Solution: A We know from Example 1 that each unit cell of metallic iron contains two Fe atoms. Number of atoms per unit cell: Contribution of Corner Spheres to Unit Cell 8 x 1/8 1 Contribution of Face Corner Spheres to Unit Cell 6 x 1/2 3 Total Contribution 1 + 3 4 Radius (r) 2/4.
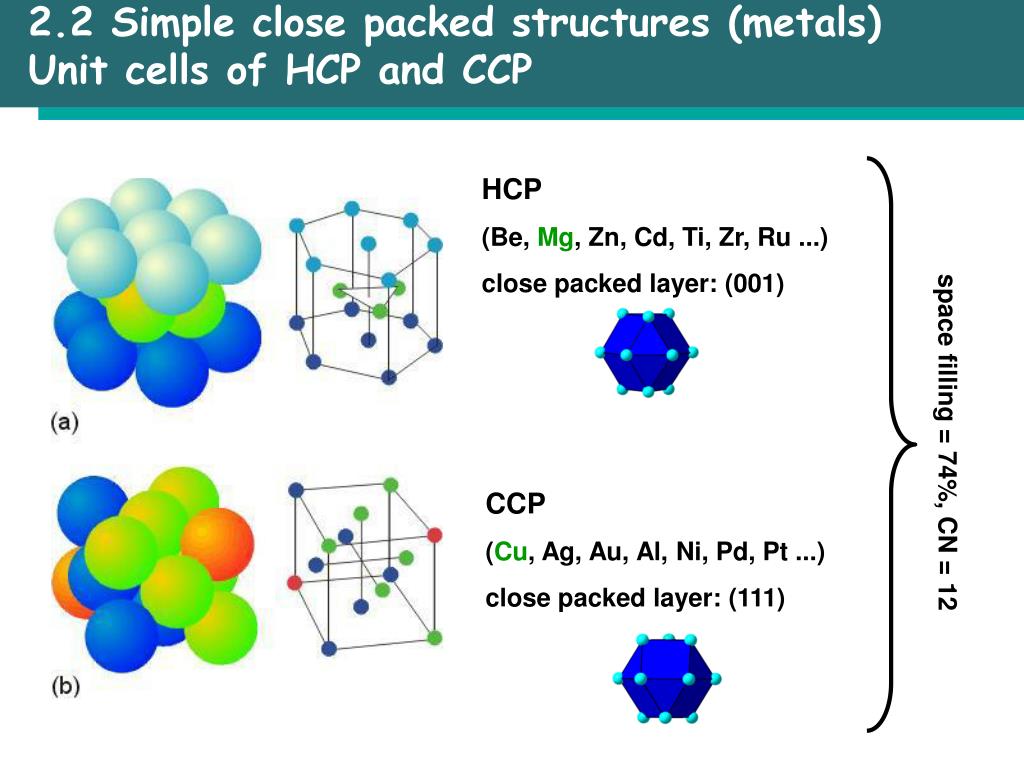
Then divide the mass by the volume of the cell. It is dimensionless and always less than unity. It is the sum of the sphere volumes of all atoms within a unit cell (assuming the atomic hard-sphere model) divided by the unit cell volume. B Calculate the mass of iron atoms in the unit cell from the molar mass and Avogadro’s number. A Simple Cubic Crystal contains only single atom and hence the Volume Occupied by atoms is given as: The Volume of Cube a3 i.e. Volume Occupied By Atoms Hcp Packing factor is the fraction of the volume of a unit cell that is occupied by 'hard sphere' atoms or ions. Packing Efficiency in CCP Arrangement = 0.7406 = 74.Illustration of the close-packing of equal spheres in both HCP (left) and FCC (right) lattices A Determine the number of iron atoms per unit cell. Volume of 2 atoms present in bcc structure 2xx4/3r3. Since one unit cell of ccp or hcp contains 4 atoms, i.e. to the volume occupied by the atoms and the closeness of the packing. The packing efficiency can be calculated by the percent of space occupied by spheres present in a unit cell. Packing Efficiency in CCP Arrangement = 0.7406 = 74.06% A FCC unit cell contains four atoms: one-eighth of an atom at each of the eight.
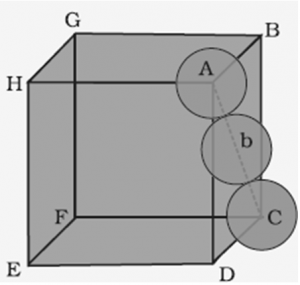
Find the formula of solid formed by M and N.

In a solid atom M occupies ccp lattice and of tetrahedral voids are occupied by atom N. Packing Fraction = ( 8 π r 3 )/(24√2 r 3)Įdge length of a unit cell be “a =2r,” and the radius of each sphere be “r”. In this arrangement, each unit cell has eight spheres at the eight corners, and six spheres at the six face centres.Ĭontribution of Corner Spheres to Unit Cell = 8 x 1/8 = 1Ĭontribution of Face Corner Spheres to Unit Cell = 6 x 1/2 = 3įormula for packing efficiency = volume occupied by the spheres per unit cell / volume of a unit cell Carbon occupies comers and face centres and also occupying half of the tetrahedral voids. ( Metal possessing it/Space occupied)'),('(A) Hexagonal cubic packing (hcp)', '(p) Iron'),('(B) Cubic. (c)Show that atomic packing factors for BCC, FCC, and hexagonal close-packed (HCP). The letters indicate which layers are the same. The outline of each respective Bravais lattice is shown in red. Comparison between HCP and FCC Figure 1 The HCP lattice (left) and the FCC lattice (right). P.E('Volume of the atoms(s) asked in Chemistry by. The fraction of the volume occupied in a unit cell, on the other. The coordination number of HCP and FCC is 12 and their atomic packing factors (APFs) are equal to the number mentioned above, 0.74. Packing Fraction = Volume Occupied by Spheres / Volume of Unit Cell packing fraction of a unit cell is drfined as the fraction of the total volume of the unit cell occupied by the atom(s). PACKING FRACTIONS 3 3 4 () 32 0.5236 a fraction a S 3 3 atoms cell 42 4 ( ) 34 2 0.7405 6 V V a fraction a S S u a 2 a CCP (and HCP) BCC 2 4 a radius 3 3 43 2 ( ) 34 0. In this arrangement, the spheres are closely packed in successive layers in the ABABAB type of arrangement.Įach unit cell has 17 spheres with radius “r” and edge length of unit cell “2r.”Ĭontribution of Corner Spheres to Unit Cell = 12 x 1/6 = 2Ĭontribution of Face Corner Spheres to Unit Cell = 2 x 1/2 = 1Ĭontribution of Spheres Inside the Unit Cell = 3 x 1 = 3Ĭontribution of All Types of Spheres to Unit cell = 6Ĭalculation of the volume of an HCP unit cell:


 0 kommentar(er)
0 kommentar(er)
